Boolean pairs: Simulating Boolean algebra with Petri-nets
In this relatively short prerequisite for my longer article on the computational power of Petri-nets, I’ll be discussing Boolean pairs, a technique for simulating Boolean algebra with Petri-nets.
Boolean pairs
I think that if you were to try to simulate propositional logic with Petri nets, then on a first attempt, you would probably try to implement it in Petri nets by using a single place for storing a Boolean value, so that if the place has a token, the value is true, and if it doesn’t have a token, the value is false. I do not believe this single-place approach can succeed, because I can’t see any way to implement the “not” operation with this design. An empty place (i.e. a “false” value) cannot give a token to another place, and therefore a false Boolean cannot make another Boolean true, which is required to simulate a NOT gate & implement the “not” operation. After realizing that this approach does not work, one might be led to believe that simulating logic operators in Petri nets is entirely impossible, but this is untrue. The key to building logic operators in Petri nets is to use a slightly different design.
Boolean algebra can be simulated in Petri-nets with the design that can be seen in the diagram below.
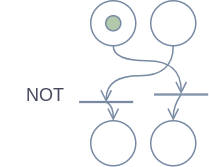
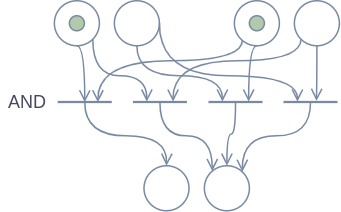
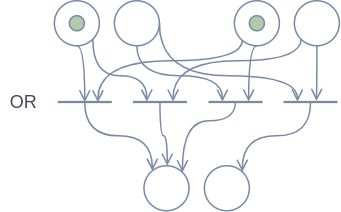
In this design, each Boolean value is represented by a pair of places instead of just a single one. I will refer to this as a “Boolean pair” in the rest of this article. For each Boolean pair, at most one of the two places may contain a token at any given moment. If they both contain a token, the Boolean pair is in an invalid state. Moreover, a Boolean pair may not contain more than one token.
One of the two places in a Boolean pair represents the value “true”, meaning that when that place has a token, the value of the Boolean is true. In my diagrams this is always the place on the left. The other place similarly represents the value “false”. In my diagrams this is the place on the right.
For simulating Boolean algebra, it is possible that neither place contains a token, and as a matter of fact this is very often the case. This essentially means the Boolean pair currently does not have a signal. I hope the figure sheds some light on what I mean by this.
As can be seen in the diagram, it is quite simple to implement the basic logic operators using this design. Logical formulas can be computed by essentially passing a few tokens along from the inputs all the way to the result of the formula. Try computing the figure’s Petri-nets in your head to get a feeling for how this all works.
The secondary operations of Boolean algebra can be constructed using a combination of the operations shown above, so it follows that Boolean pairs are sufficient to simulate the entirety of Boolean algebra.
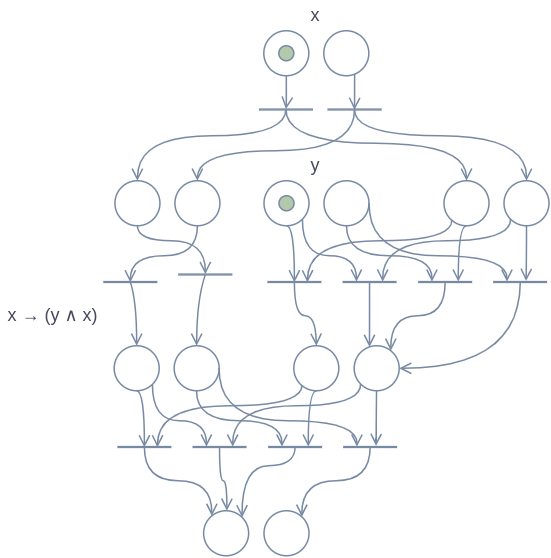
These next diagrams are examples of how you would simulate a more complex formula, with multiple subsequent operations.
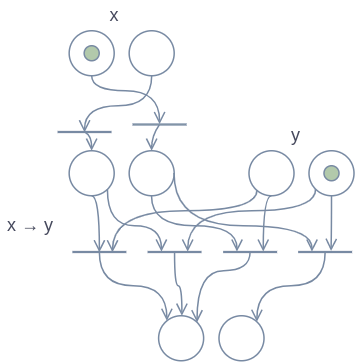
This last formula below contains multiple appearances of one variable. I chose to add a part to the top of the diagram which copies the value of that variable to all of the places where it appears in the formula. This isn’t necessary — we could simply start with the value in all of those places —, but I thought it would be good as an example of how to structure it in a modular way, since this way this Petri-net can be incorporated into an algorithm consisting of multiple formulas.